Research
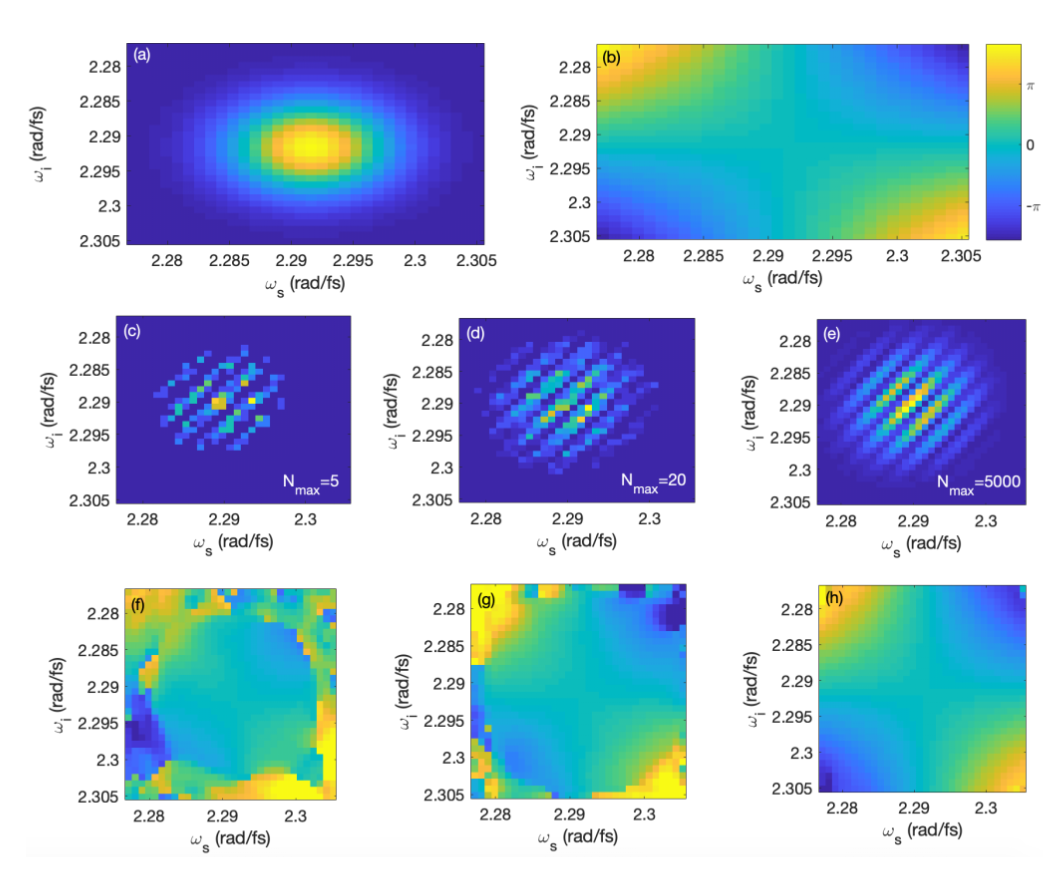
Encoding information in the time–frequency domain offers a versatile and efficient platform for quantum information processing. It provides a novel scheme for communications with large alphabets, computing with large quantum systems, and new approaches to metrology. It is hence crucial to secure full control on the generation of time–frequency quantum states and their properties.
Biphoton states generated for instance through SPDC sources can exhibit correlations in time and frequency, making it necessary to reconstruct their joint spectral profile and phase. Characterizing the spectral phase in particular poses a great challenge, one that has similarly been taken up by classical ultrafast metrology to control ultrashort pulses in the femtosecond and attosecond timescales.
Related Publications
I. Gianani - “Robust spectral phase reconstruction of time-frequency entangled bi-photon states” Phys. Rev. Research, 1, 033165, 2019
The importance of networks as a model to describe complex systems cannot be overstated. They are used to describe social interactions, biological processes, transport phenomena, and physical systems alike. In the context of quantum technologies, networks constitute the underlying structure of communication and computation protocols. Understanding how quantum information can be reliably transmitted between distant nodes, or routed among different computational units is a key step in development of secure communication schemes and fast computation protocols.
QWs are the natural paradigm to study how quantum information is distributed across these networks. Walkers can be used as quantum probes for the estimation of parameters, allowing to take advantage of estimation theory stemming from quantum metrology. In this framework, the amount of extractable information from a system is upper bounded by the Quantum Fisher Information. This allows to cast the information distribution problem using a quantifiable figure of merit, leading to a reliable characterization of the network properties.
In order to explore the realm of large complex networks from an experimental perspective, it is necessary to identify a platform enabling quantum walks with great tailorability and scalability, allowing access to long-time dynamics on the network, hence involving a great number of nodes. In this regard, realising simulated quantum walks that can be controlled and easily modified to explore different configurations, is an ideal solution.
Networks in the spectral domains answer all the above-mentioned requirements. Furthermore, the way in which the walk is simulated on these networks opens up intriguing possibilities. Indeed, while it is possible to control the available experimental parameters to simulate linear quantum walks, they also allow to simulate more involved evolutions on the network, that are nontrivially recognizable. This poses a further question compared to the mere characterization of the network: can we trace back and identify what evolution the network has incurred, starting from its state at different times? This question naturally leads to incorporating a machine learning approach in our research, with the development of Hamiltonian learning algorithms capable of providing a rapid answer to this problem.
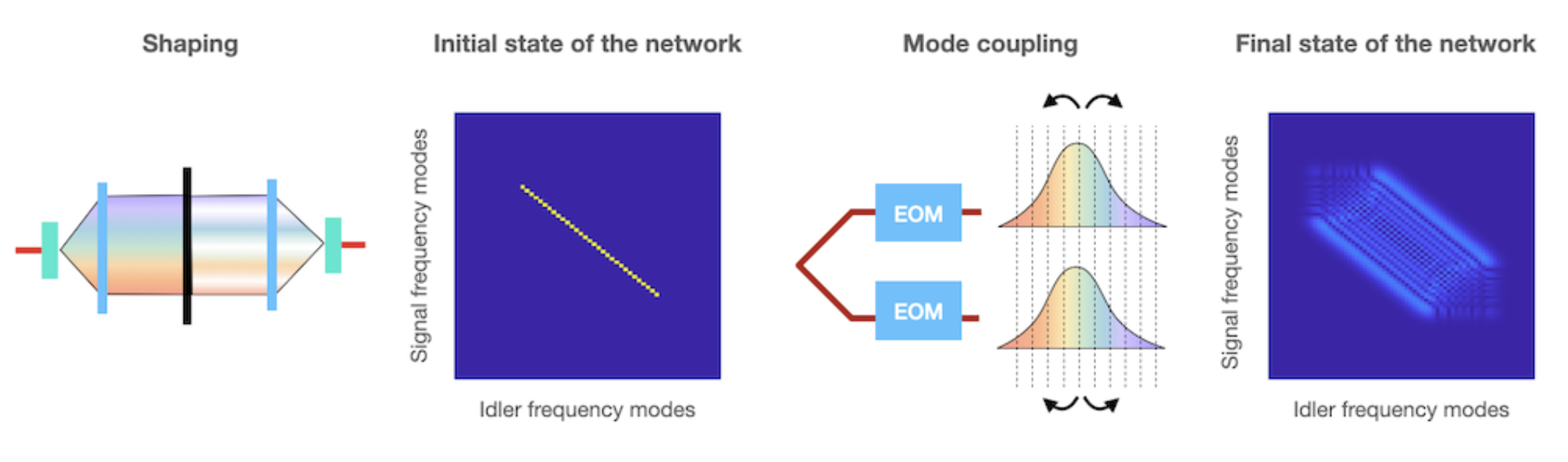
The generation of photons through spontaneous parametric downconversion (SDPC) can, if properly tailored, allow to obtain anticorrelations between the generated photons resulting from energy conservation. At the same time it grants access to a large two-dimensional network where each node is identified by the frequencies of the two photons, whose space is conventionally discretized when performing a measurement. Accessing these features however requires a thorough characterization and control of the photon spectral properties, i.e. the joint spectral amplitude and phase, a task akin to the spectral characterization of classical ultrafast pulses. Full characterization of the spectral state allows to shape the initial state of the network with specific control on its entanglement, hence opening up a vast playground for exploring the effects this has on its evolution on the frequency network.
Related Publications
C. Benedetti, I. Gianani, "Identifying network topologies via quantum walk distributions”, AVS Quantum Science 6, 014412, 2024I. Gianani, C. Benedetti, “Multiparameter estimation of continuous-time Quantum Walk Hamiltonians through Machine Learning”, AVS Quantum Science 5 (1), 014405, 2023
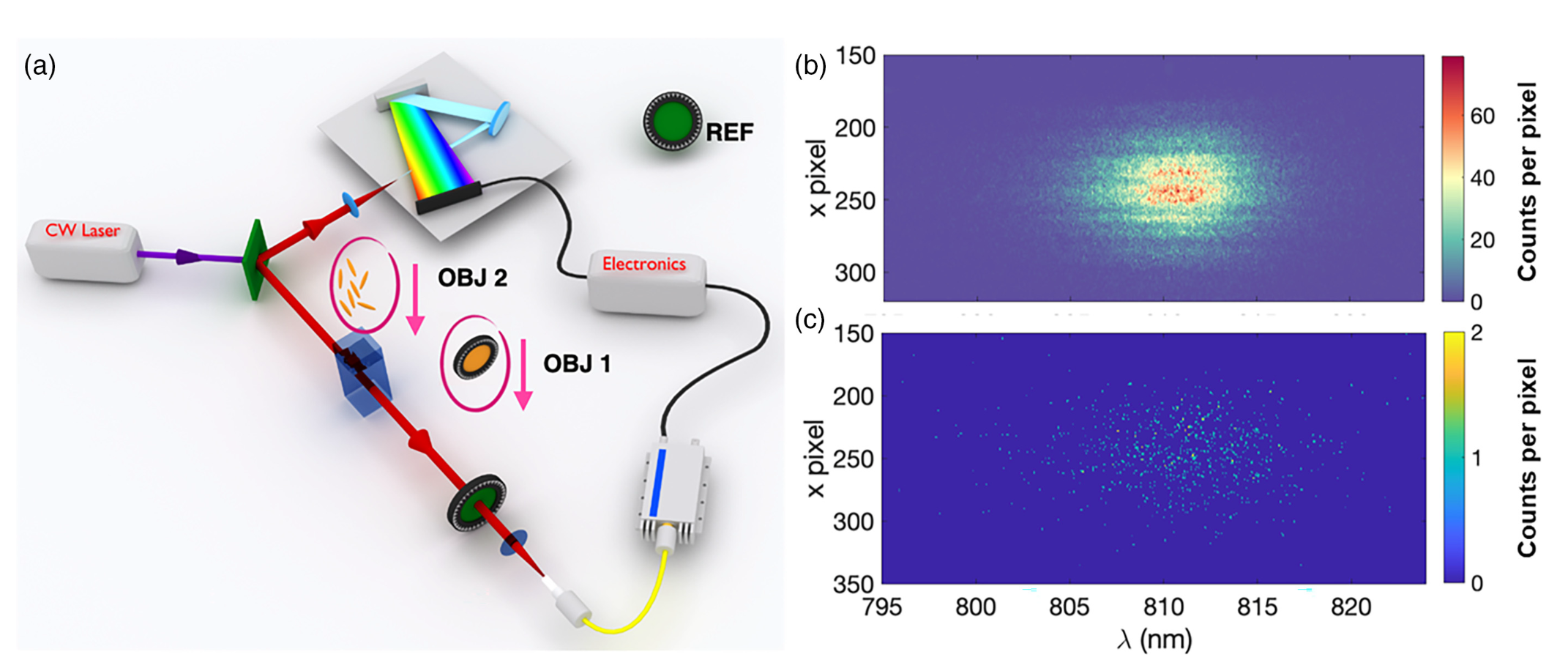
Quantum spectroscopy leverages the unique properties of quantum light, such as entanglement, to achieve superior spectral resolution compared to classical light sources and to address technical requirements such as that of performing the measurements remotely.
Related Publications
A Chiuri, M Barbieri, I Venditti, F Angelini, C Battocchio, MGA Paris, I. Gianani, "Fast remote spectral discrimination through ghost spectrometry”, Physical Review A 109 (4), 042617, 2024M. Barbieri, I. Venditti, C. Battocchio, V. Berardi, F. Bruni, I. Gianani, “Observing thermal lensing with quantum light”, Optics Letters, 49,5, 1257-1260 (2024)
A. Chiuri, F. Angelini, S. Santoro, M. Barbieri, I. Gianani, “Quantum Ghost Imaging Spectrometer” ACS Photonics, 10, 12, 4299-4304 (2023)
I. Gianani, LLS Soto, AZ Goldberg, M Barbieri "Efficient lineshape estimation by ghost spectroscopy”, Optics Letters 48, 3299-3302 (2023)
I. Gianani, M. Barbieri, F. Albarelli, A. Verna, V. Cimini, R. Demkowicz-Dobrzanski, “Kramers-Kronig relations and precision limits in quantum phase estimation”, Optica,8,12, 2021
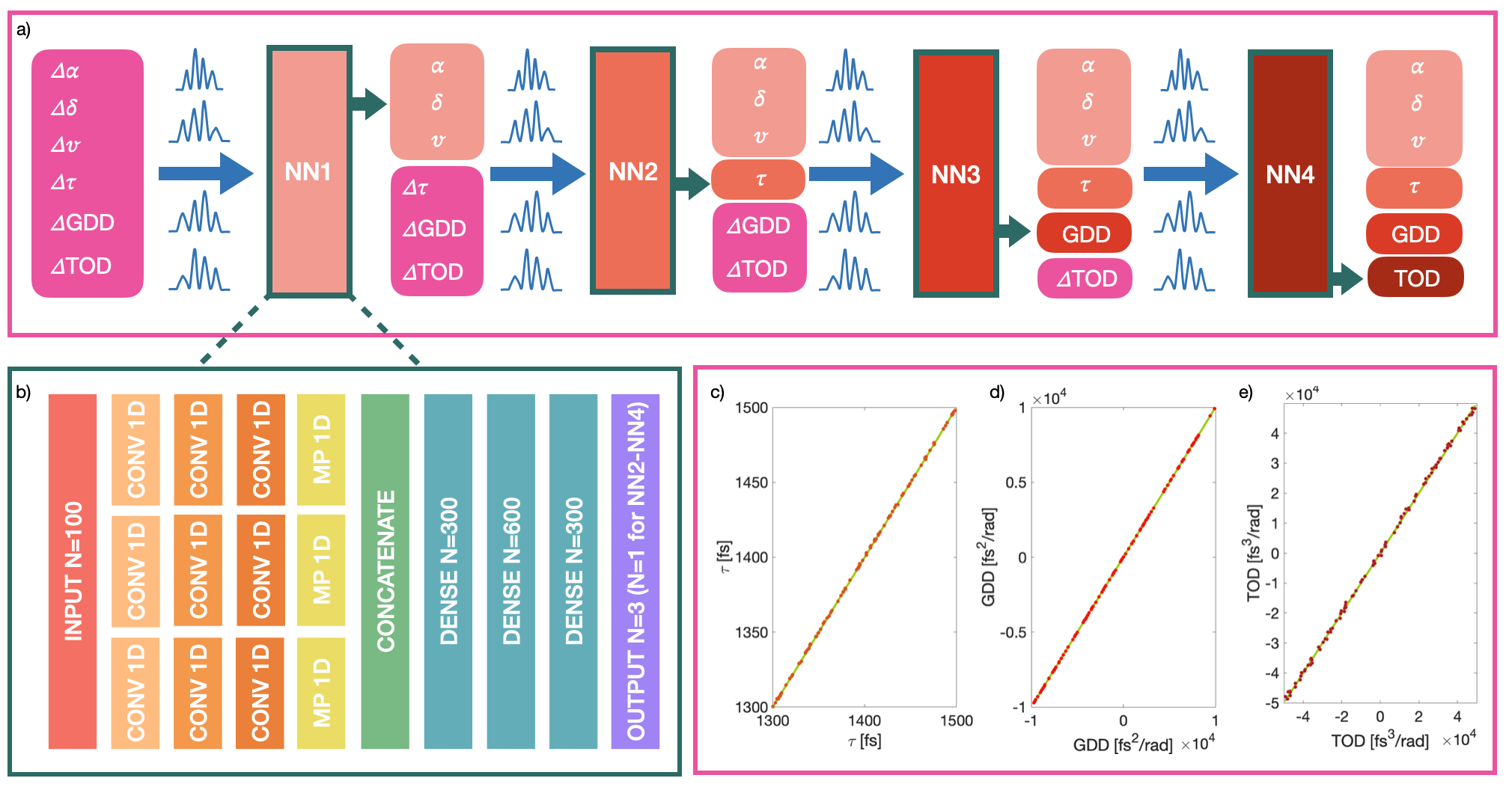
Machine learning has emerged as a powerful tool in quantum optics, where it is used to optimize complex experiments and improve data processing. In this research area, machine learning algorithms are applied to tasks such as calibrating quantum sensors and estimating parameters in quantum systems. By combining quantum technologies with machine learning, one can enhance the performance of quantum devices and develop new ways to analyze quantum information. Indeed, all the previous research lines presented in this page do greatly benefit from the use of ML techniques, may that be as unbiased estimators for recovering the parameters of a network, as a calibration and spectral analysis tool for spectroscopy sensors or as a way to retrieve the spectral phase of classical and quantum states.
Related Publications
I Gianani , IA Walmsley, M Barbieri - SPIDERweb: a neural network approach to spectral phase interferometry, Optics Letters 49 (19), 5415-5418, 2024.V.Cimini, I. Gianani, N. Spagnolo, F. Leccese, F. Sciarrino, M. Barbieri “Calibration of quantum sensors by neural networks” Phys. Rev. Letters, 123, 230502, 2019
I. Gianani, I. Mastroserio, L. Buffoni, N. Bruno, L. Donati, V. Cimini, M. Barbieri, F. S. Cataliotti, F. Caruso, “Experimental Quantum Embedding for Machine Learning”, Advanced quantum technologies, 2100140, 2022.